Black Holes -- An Astronomical Myth

Physics is often a quest for the exotic truth. With many such truths having been discovered in the last century, our need for them has intensified like a drug addiction. Now we often find truth to be not exotic enough. So we settle for the exotic that has little to do with the truth. Einstein's theory of gravity was considered quite exotic at one time. But now we need to ratchet up the "exoticness" with things like black holes. Here I will try to present the "unexotic" truth or the lack thereof in the popular understanding of black holes.

How do I identify a black hole?

Well, how do I identify a nose? When I was young someone must have shown me my nose (and those of others) and told me what it was called. So now, whenever I see a nose, I quickly identify it as such. This is how we all identify most things we see around us. We remember definitions of objects by observation -- let us call this kind of definition a "definition by observation". Then whenever we see a new object we match it with existing definitions in memory.

Unfortunately, the definition of a black hole is not a definition by observation. It is a "definition from theory" -- the theory of general relativity to be precise. This makes identification of a black hole a bit more tricky. General relativity is the theory of gravity as presented by Einstein. It is an improvement over the earlier theory of gravity presented by Newton. It is an improvement because it explains several astronomical observations in the solar system much better than the Newtonian theory. With such spectacular success in the solar system it is natural to want to test the theory beyond the solar system. We must remember here that a theory is only as good as the experiments it explains. So we need some theoretical predictions of Einstein's theory that can be tested experimentally beyond the solar system. Enter the black hole -- a theoretical prediction of general relativity in need of experimental verification. Hence, I conclude that the definition of a black hole comes from theory rather than observation. So, to identify an object as a black hole, we must make sure it matches with the definition from theory and remember that there exists no definition from observation. Moreover, the existence of a theoretical definition does not guarantee the existence of such objects. Only experiment can tell for sure.

Black hole -- the definition from theory.

As one may expect, this theoretical definition of a black hole is deeply mathematical. In the following I shall present some possibly observable effects of the mathematics.

The simplest black holes are spherically symmetric. For any spherically symmetric object (may be a star) one may define an imaginary sphere around it of radius r_s = 2GM/c², where G (= 6.67 X 10^-11 Nm²/kg²) is the universal gravitational constant, M the mass of the object and c the speed of light in vacuum. r_s is called the Schwarzschild radius. If all the material of the object is within this imaginary sphere (that is if the surface of the object is at a radius less than r_s) then this imaginary sphere is called the event horizon and the object is called a black hole. Note that if the radius of the surface of the object is larger than r_s then there is no event horizon and the object is not a black hole.

Now, let us see what the big deal is about this event horizon. The region within the event horizon is usually referred to as "inside the black hole". But first we need to understand all the oddities of the horizon itself. If you stand outside the black hole and watch a clock (or watch) placed precisely on the event horizon, it will appear to have stopped. More generally, if you put a clock in a spaceship and let it fall towards the black hole while you watch it from outside, the clock will appear to progressively slow down. This is the so-called gravitational time dilation. Theoretically, this time dilation becomes infinite at the event horizon (the clock stops). However, this time dilation also makes the spaceship itself fall slower as it gets closer to the event horizon. So, it takes an infinite amount of time to reach the horizon (as seen by you the outside observer) -- which really means that it never gets there. On the other hand, if there is an astronaut in the spaceship, he/she will find the clock working quite normally. Hence, according to the astronaut the spaceship will reach the horizon in finite time and then proceed to go inside the black hole quite eventlessly (provided there is some technology to prevent the spaceship, clock and astronaut from coming apart due to strong gravitational tidal forces!).

While you, the outside observer, watch the spaceship clock getting slower, your own clock is running quite normally (according to you). So, by the time the spaceship clock reaches the horizon, your clock has run out of time (reached infinity in time!). This means whatever happens to the spaceship after it enters the black hole is unseen by you -- hence the name "event horizon". The astronaut, of course, does not reach infinite time at the horizon and hence gets to see what is inside the black hole.

For a rough idea of the Schwarzschild radius, one may compute that of our own Sun. It turns out to be about 3 kilometers. The actual radius of our Sun is about 7 hundred thousand kilometers. So, if this huge bulk is squeezed into a 3 kilometer radius sphere, we would have a black hole.

Myth #1 -- A Black hole can be identified from outside its event horizon.

General relativity shares an interesting feature with its predecessor (Newtonian gravity). The gravitational field outside a spherical star depends only on its mass and gives no clue about its size. What this means is that if our Sun were to suddenly shrink tomorrow (even to black hole dimensions), the planetary orbits would remain unchanged.

This is quite a disappointment for the art of black hole identification. As long as you look at phenomena outside the star and outside the expected event horizon, all gravitational effects will be the same whether the star radius is greater or less than the Schwarzschild radius r_s. Hence, from outside the star one cannot tell if it is collapsed down to its black hole size or not. So, the only way to determine whether a star is a black hole or not would be to send a probe inside it. But we would have to wait literally forever (infinite time) for the probe to even reach the event horizon, let alone go in and return.

Now, I know many claims have been made of observed black holes. The arguments given involve very strong gravity near some stars which produce all kinds of violent activity and what is more there is darkness near the center. But all of this can happen just as well near a very heavy star that is still not a black hole. We have to remember that the definition of a black hole is mathematical and that mathematical definition must be fulfilled before anything can be called a black hole. If we were to take to qualitative definitions like "a black hole looks dark in the middle and sucks up everything around it," we would soon find black holes in our toilets.

Myth #2 -- Some stars can collapse to become black holes.

The popular story is that in a supernova large amounts of mass can get crushed at the center to form a black hole. Well, general relativity disagrees. Think of a black hole being formed by a certain amount of mass M in the form of a fine dust (debris) collapsing due to gravity. It will become a black hole when all of M falls within a sphere of radius r_s = 2GM/c² as given above. But closer it gets to doing this the greater is the time dilation for the outermost pieces of the debris. The last few pieces that need to fall in to form the black hole will take literally forever (infinite time) to do so. Hence, a star cannot collapse to form a black hole. What it can form is a ball of dust which is close to being a black hole at every spherical layer within it but not quite. In such a star, time dilation is so large for every falling piece of debris that it appears to be "frozen" in time. It can be shown that such a "frozen star" would have a density profile that reduces as the inverse square of distance from the center.

So, the only way the universe can have black holes is if they were there all the time. Of course, this is a conclusion of general relativity which is only a theory and a theory can be wrong. However, if general relativity is wrong and we need to abandon it, we would also have to abandon the definition of black holes that comes from it and there exists no other definition.

Myth #3 -- Black holes must be very heavy and dense.

The only condition that a black hole needs to satisfy is the mathematical one given earlier. This definition does not provide any critical mass or density for a black hole. A jug of water (say 1 kg) could become a black hole if squeezed down to a sphere of radius 1.5 X 10^-27 meters (its Schwarzschild radius). At the same time the lightest element hydrogen at standard temperature and pressure could form a black hole if one were to gather up a ball of the gas of radius 4.3 X 10¹³ meters.

The myth started because of a kind of star called white dwarfs. These are stars that cannot collapse any further because of a quantum mechanical effect (Pauli exclusion principle). This effect does not allow more than one electron in any given quantum state. When gravity tries to collapse a star beyond a certain limit, it tries to force electrons into identical quantum states. To avoid this, the electrons generate a reverse pressure that prevents the star from collapsing any further. However, if the mass of the star is beyond a certain limit (called the Chandrasekhar limit), the gravitational forces are strong enough to make the electrons combine with protons to form neutrons. Then there are no more electrons left to produce that reverse pressure and hence stars heavier than the Chandrasekhar limit do not stop collapsing at the white dwarf stage. But then the neutrons in such a star (called a neutron star) also obey Pauli exclusion principle and they produce a new reverse pressure to hold up the star. At this stage some have tried to repeat the Chandrasekhar limit idea and figured that beyond a certain limiting mass even a neutron star will collapse further -- this time into a black hole. This is where the reasoning gets a bit fuzzy. Unlike the earlier mechanism of electrons combining with protons, there is no known nuclear process by which neutrons can combine with anything to cheat Pauli exclusion principle.

But there is really no need to figure out mechanisms of collapse of neutron stars. A neutron star, without any further collapse, could be a black hole (if it has enough mass). For that matter a white dwarf or even a big ball of hydrogen could be a black hole. The reason none of these will actually collapse to become a black hole is the infinite time dilation problem discussed above.

Myth #4 -- Nothing (not even light) can escape from a black hole.

From the point of view of the outside observer, nothing (not even light) ever enters the black hole. So, the question of escape is quite moot in this case. Hence, the question of escape must be from the point of view of the astronaut (and his/her spaceship) falling into the black hole.

The equation of motion (a differential equation) of any small object (an unpowered spaceship in particular) moving around a black hole as seen by an observer on the object can be found in any general relativity text book. It is sometimes called the geodesic equation as the trajectories of objects moving under the influence of gravity alone are called geodesics. Sometimes these trajectories are also called free fall trajectories as an unpowered spaceship will "fall" along these trajectories. The geodesic equation is time-reversal symmetric -- which means that if the unpowered spaceship could "fall" from point A to point B it can also retrace its path back from point B to point A if somehow one could reverse its momentum at point B. As points A and B could be anywhere in general, one could pick point A outside the black hole and point B inside it. This means that if one can go from outside to inside the black hole, one can just as well go the other way if somehow the momentum direction can be reversed. The reversing of momentum requires a finite change in momentum and as it can be done in nonzero time, it can be done by a finite amount of force. This force, of course, has to be nongravitational in nature. It is also expected to be huge. But as long as it is finite, no laws of physics are violated. So one may picture this spaceship with a tiny passenger capsule and a huge fuel compartment that falls freely from point A to B. When it reaches point B the rocket engines start and all the fuel is burnt to produce enough nongravitational force in order to reverse the momentum of just the tiny passenger capsule. Once its job is done, the fuel compartment itself can be ejected allowing the passenger capsule to follow the geodesic backwards and return to point A outside the black hole. Hence, we have escape from a black hole!

The above proof may seem qualitative, but it is actually mathematically complete. I did not have to write down the actual equation because the only aspect of the equation that is relevant to the proof is the time-reversal symmetry.

The "no escape" myth has established itself in literature due to a misinterpretation of a unique feature of geodesics within a black hole. Consider a black hole that has all its mass concentrated at the center. It can be shown that a geodesic entering the black hole at any angle is doomed to spiral into the center. This is in contrast to geodesics that remain outside the black hole. Such outside geodesics can reach a nearest point of approach (from the center) and then move away. This is like paths of comets that come close to the Sun and then move away. However, one must realize that geodesics are paths of freely falling objects only. So, an unpowered spaceship will truly fall to the center of the black hole once it crosses the event horizon (to be precise, once it gets any closer than 3r_s/2 from the center). But as soon as the rocket engines of a spaceship are fired nongravitational forces are applied and the spaceship no longer follows a geodesic. Once the momentum of the spaceship is reversed the rocket engines are turned off and the spaceship is free to follow a geodesic which now happens to be the old geodesic in reverse.

In case a general mathematical proof has not convinced you, I have a computer program for you to play with. It solves the geodesic equation numerically and plots the trajectory of a spaceship if the launch conditions are given.

To download the program click here.

An example of a trajectory plotted by this program is shown below. The red spot is the launch position -- the point B inside the black hole. The green circle is the event horizon. This is an escaping spaceship!

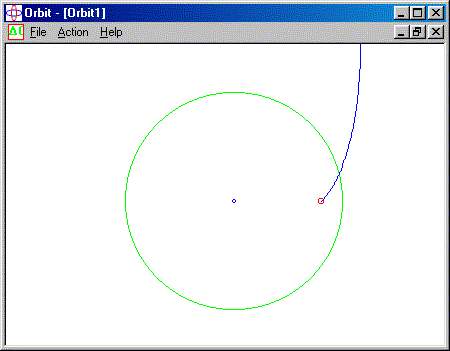
However, there is one little problem. The astronaut (in the spaceship) who went from point A to point B saw the outside observer's time go to infinity when he/she reached the event horizon. So what outside observer time will the astronaut return to after he/she goes into the black hole and returns? General relativity has no answer. This allows us to conjecture freely and create all kinds of science fiction. For example, the astronaut may reappear in a whole new universe with a whole new time line.

The reason for the failure of general relativity here is in its "local" nature. This means that all equations of general relativity are differential equations that hold true at individual points in space-time. When we have to come up with large scale solutions, we merely "tack" on these individual point solutions. Such an approach can get into trouble when the topology of space-time is not simple. For example, for cosmological predictions of general relativity, we need to make ad hoc assumptions about the topology of the universe. General relativity cannot tell us what it should be. In the case of black holes the weird thing is that the astronaut's time line and the outside observer's time line do not have corresponding points everywhere. The infinity of the outside observer's time line maps to the astronaut's time at the point of entry into the black hole. The astronaut's time line clearly has points beyond this point but the outside observer's does not. This mismatch of time lines is a topological one and cannot be addressed by general relativity. However, all such problems would disappear if we assumed that black holes did not exist since time began. As I have shown that new black holes cannot form in finite time, this would make sure that there are never any black holes. Besides, as we cannot identify a black hole from outside, it may not make much physical sense to talk about them anyway.