Taking The Bang Out of the Big Bang Theory
by Tarun Biswas (June 22, 2007)
A Catastrophic Beginning
The idea of "Genesis" is not unique to the Bible. Other religious texts have similar explanations of "The Beginning". Now Physics, in its transition towards becoming a religion, also provides its own version of the story -- The Big Bang Theory. From a sociological point of view, it is interesting to investigate this need for a catastrophic beginning. Probably, it stems from an urge to find a parallel to an individual human beginning -- human birth is quite catastrophic.
In earlier days physicists were happy to explain directly observed phenomena using simple theories like Newton's laws and electrodynamics. Currently, for some odd reason, we have taken upon ourselves the job of explaining everything. This is a tall order -- particularly because it would require us to know everything that occurs in the universe. We are insignificantly tiny little beings on an insignificantly tiny planet trying to gather information about the whole universe. I think some humility is in order here! The Big Bang Theory shows a dramatic lack of such humility. Real data is much too sparse to come up with any theory at all about the evolution of the universe. Nonetheless, if we still insist on coming up with such a theory, at least we should keep it within the bounds of science. In the following, I shall show how the Big Bang Theory has stepped outside the scope of science. The evidence that is supposed to support the theory really does not. Besides, there is evidence against it.
Stepping Outside the Scope of Science
Science, in particular physics, is about measurable quantities. Theories may often define abstract quantities (like the wavefunction in quantum theory) that have no directly measurable meaning, but they always present a connection between these abstract quantities and actual measurables. However, the Big Bang Theory claims that, at the instant of the Big Bang, actual measurable quantities like temperature had as their measurable value an exact infinity! This is scientifically meaningless. There are no measuring devices that can measure an exact infinity -- even thinking about such a device is meaningless. Of course, we often approximate large measurements to be infinity. But we are always aware of the fact that it is just an approximation. An exact infinity for a measurement is still quite meaningless.
Also, all physical objects have finite sizes in all three spatial directions. Once again, we sometimes approximate objects as having zero size in one, two or even all three spatial dimensions. One often talks of a "point" object (or particle) when the internal motion of the object is inconsequential for certain purposes. But it is always understood that such a point object is just an approximation. The Big Bang theory considers the whole universe to have been an exact point object (no approximation) at the initial instant! This is quite unphysical.
A Prediction of General Relativity?
The idea of the Big Bang came from General Relativity (GR). However, to say that GR predicts the Big Bang might be too strong a statement. Several ad hoc assumptions have to be added to GR to produce the Big Bang. The plausibility of these assumptions is often debatable. So, let us see what GR can or cannot predict as well as what it does or does not predict.
A critical observation about the theory of GR is the so-called local nature of its field equations (Einstein's equations). This means that GR can compute gravitational fields only in small regions of space-time at a time (local solutions). Of course, one can "sew" such small regions together to get large regions (global solutions). In fact, this locality of field equations is true for all theories of physics. But it has not been a problem before GR came along. The notable difference for GR is in the ability of the field to produce curvature of space-time. This complicates the process of "sewing" together local solutions to obtain global solutions. And global solutions cannot be obtained all at once as the equations are local. Hence, if space-time itself is curved, we need to know the basic shape (or topology) of the universe before we can find solutions to Einstein's equations in local patches and "sew" them together. So, topologically, is the universe spherical, cylindrical, toroidal (donut shaped) or any other exotic shape? Einstein's equations give no clue in this matter. Hence, one makes a plausible assumption -- the universe is a four-dimensional cylinder. The axis of the cylinder is the time axis and three-dimensional space wraps around the axis as a three dimensional sphere (the surface of the sphere itself is three dimensional unlike the two dimensional surface of the usual sphere). This assumption is considered plausible because it allows for a constant curvature of space alone and we have no information to show any preferred directions or positions in space. Time is assumed to go along the axis because time going around in a closed loop does not make physical sense. It is difficult to argue against this assumption about the shape of the universe. But it must be noted that it is not a result of GR.
Once the shape of the universe is chosen, can we go ahead and solve Einstein's equations in GR? Well, not quite -- more assumptions are needed. Einstein's equations, like the equations for electromagnetic fields, require the knowledge of the source of the field. Theoretically, this source is called the stress tensor. Experimentally, we have very little clue as to what it should be. Note that all experimental tests of GR have been conducted for solutions of Einstein's equations with zero stress tensor (i.e. vacuum). So, we are once again left guessing as to what this thing called stress tensor should be. There are some theoretical constraints -- but the possibilities are still infinite. So, we draw analogies from electromagnetic theory. There, a similar mathematical object is related to density of energy and momentum. Here, we expect the source to be related to mass and we already know about mass-energy equivalence. So, we pick a quantity that is related to density of energy (or mass) and momentum of objects (galaxies) in the universe. These galaxies are assumed to be like "dust" particles that do not exert forces on each other.
So, are we there yet? Are we ready to solve Einstein's equations? Not quite -- we need a few more assumptions -- the initial conditions. If one were to summarize the goal of physics in a single statement, it would be "to predict the future using current information." Newton's second law, the Schroedinger equation and Maxwell's equations were all designed with this goal in mind. Mathematically, these equations are often called Initial Value Problems (IVP). It means that these equations can be solved to find future observables if certain quantities are known at one initial instant of time i.e. the initial conditions. Einstein's equations also define an IVP. So, we need initial values of the field (and some related quantities) at some initial time at all points in space. Clearly, such initial data is impossible to gather. So, once again, we need to make plausible assumptions about quantities like the size of the universe and mass density.
To add to our troubles, Einstein himself was double minded about including a constant term (called the "cosmological constant") in his equation. The value of this constant is also open to measurements that are difficult to make. Some (including Einstein) are uncomfortable about using this constant. For them, it may or may not be of comfort to know that a constant "pressure" term, if included in the stress tensor, is mathematically equivalent to the cosmological constant. However, this pressure term can be quite bewildering in itself, as it does not act like what is physically understood as pressure. It is known that if the pressure of air inside a balloon is increased it expands. But increasing the pressure term in the stress tensor actually has a contracting effect on the universe! Nonetheless, all these unknown initial conditions give us something to play with and see what fits known data. Various possible scenarios can fit the data. The following graph shows the size of the universe (R) versus time for some of these scenarios.
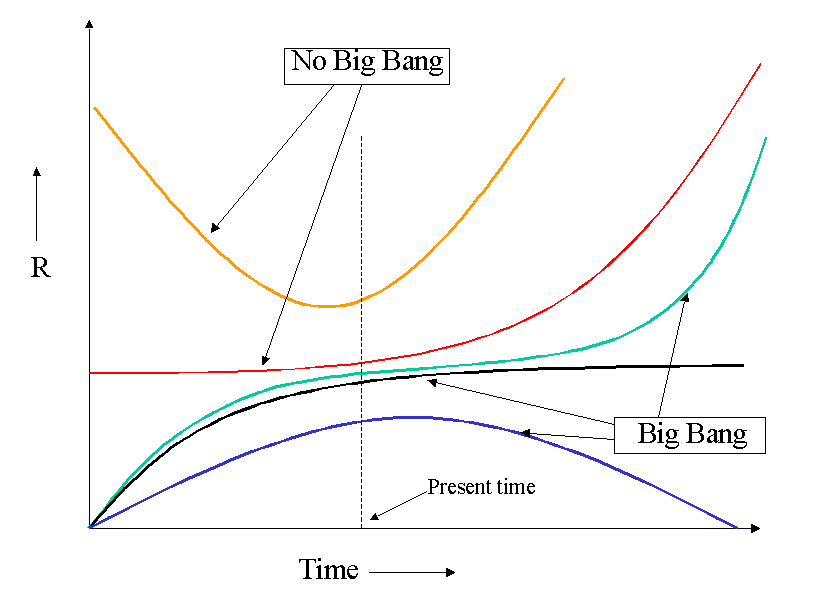
Note that some of the possibilities do not require the universe to be exactly zero in size at any time (No Big Bang)! This avoids having exact infinities for measured quantities. Of course, we also notice that some other possibilities do require a zero size at some instant of time (Big Bang). In normal physics, when equations have some physical solutions and some unphysical solutions (exact infinities for measurables), it is customary to drop the unphysical ones. However in this case, quite amazingly, it is the unphysical Big Bang solutions that are selected as correct and the ones without infinities are ignored!
Inflation?
The exact infinities of the Big Bang are often explained by suggesting that quantum physics will fix the problems. After all, quantum mechanics describes systems of small scale and the universe must have been very small at the time of the Big Bang. This invited particle physicists to try their hands at the game. They realized that the Big Bang meant extreme high energy phenomena -- energies at which the conjectures of the Grand Unified Theories (GUTs) would be in effect. Using these theories, it was explained that the universe expanded much faster during the first fractions of seconds after the Big Bang than what was expected from GR. This process was called "inflation". This also explained why the universe is relatively uniformly spread as far as we can see from Earth. However, these are only conjectures as there are no independent verifications of GUTs.
Besides, this still does not get around the exact infinities at the instant of the Big Bang.
The Hubble Red Shift?
The idea that the universe is expanding came from Hubble in 1929. Wavelengths of certain characteristic light emissions from stars seem to be longer for stars that are farther. As red is the longest wavelength light we can see with our eyes, this phenomenon of elongating wavelengths is seen as a shift towards red -- hence, the name "red shift". Earthbound experiments on any kind of light shows that such red shift occurs for light sources that move away from the observer -- greater the speed, greater the red shift. This is called the Doppler shift. Hence, one can argue that farther a star is from Earth, greater is the speed with which it recedes from us. GR models agree that the red shift is due to recession velocities of stars, but it is not quite the Doppler effect. Waves of light are elongated because the space through which they travel is itself expanding. Farther a star is, longer is the time the light from it spends in transit and hence, greater is the red shift.
Although this is indirect evidence, it is strong enough for us to believe that the universe really is expanding. But there is still no evidence that the universe has always been expanding starting from zero size. The graph shown above gives one GR possibility (yellow line) that allows the universe to have first contracted and then come to the present state of expansion. Another GR possibility (red line) allows the universe to always expand without ever having been of zero size.
What About the 3 K Background Blackbody Radiation?
In 1965 A. A. Penzias and R. W. Wilson reported a fascinating experimental result -- the Earth is receiving uniform electromagnetic radiation that is not coming from any known objects like stars and galaxies. The amount and nature of this radiation is quite independent of direction in space. Also, the spectrum of the radiation (primarily in the microwave range) mimics what is theoretically and experimentally known to be blackbody radiation. Blackbody radiation is produced by what is known as a blackbody (of course!). Theoretically, a blackbody is an object that absorbs 100% of any electromagnetic radiation that falls on it. Experimental approximations of such an object can be quite good. Now, if a blackbody is heated to any temperature it is known to produce its own electromagnetic radiation. This radiation is characterized by the blackbody's temperature alone. Hence, if the spectrum of the radiation is known, the temperature can be calculated. The data of Penzias and Wilson suggested a temperature of about 3 degree Kelvin (270 Celsius degrees or 486 Fahrenheit degrees below the freezing point of water).
Theoretical analysis shows that the characteristic nature of the spectrum of a blackbody is due to the thermal equilibrium of radiation within it. Hence, all that one can conclude from the observations of Penzias and Wilson is that the universe contains radiation in equilibrium at 3 degrees Kelvin. By itself, it says nothing about the universe expanding and definitely not anything about a Big Bang. If the Hubble expansion is brought into the picture, one can conclude that the temperature of the background radiation must have been higher at an earlier time. Gamow, Dicke and others have argued that if the universe were smaller at earlier times, its energy density must have been higher -- assuming that total energy is conserved. As energy density is directly related to temperature, this means an expanding universe must be cooling with time. Hence, tracking back in time we find a time when the temperature was so high that atomic nucleii could not stay together and came apart into their constituents. It is possible to roughly estimate this time by knowing the rate at which nucleii form as temperature decreases and the current amounts of such nucleii in the universe. This time is seen to roughly agree with the 3 degree temperature of the current universe, if some assumptions are made about the temperature at which nucleii came apart.
Then comes the big leap of faith of the Big Bang model -- if the universe has been expanding since the first nucleii were created, then it must have been expanding before that when the first quarks and leptons were created and even before that when all matter was in the form of radiation and still before that when the universe was a point of axactly zero size! Notice that all of these arguments are based on conservation of energy -- an earlier smaller universe had a higher temperature because total energy must be conserved. Now, the proponents of the same idea turn around and say that the whole universe was created at one instant of time when all its energy appeared out of nowhere all at once -- a rather catastrophic violation of energy conservation principles!
Dark Matter and Dark Energy?
Earlier I have mentioned the stress tensor as the source of gravitational field according to General Relativity. I have also mentioned that very little is known about its directly observable aspects. Hence, it is commonplace to assume that it is whatever it must be to produce observed gravitational fields. In other words we are free to throw in the kitchen sink (and a bathtub or two while we are at it) into this stress tensor as long as we can generate observed gravitational fields from it. Although I joke about it, this is a serious method of building physical theories and it has worked well in the past. A better understanding of the stress tensor is expected to come from such attempts at explaining the field.
The part of the stress tensor that is due to the mass of the "dust" of galaxies is the best understood. However, there does not seem to be enough of this dust directly observed to fit the current Big Bang model. This is not a problem, as there could always be stars and galaxies in the universe that produce no observable radiation and hence, are invisible. Such objects constitute what is known as "dark matter". Some indirect evidence has been found to support the idea of dark matter. For example, the observed rotation speeds of galaxies seems to be too high for the directly observed masses. Hence, there is a possibility that dark matter is responsible for this. But note that the existence of dark matter itself is not evidence for the Big Bang. Also note that the nature of this dark matter does not have to be exotic -- e.g. black holes, WIMPs, etc.. It could be literally "dark matter" -- i.e. matter that does not radiate anything. If our Earth were to escape from the Sun, it would be such a dark object as it produces very little radiation of its own (Well, the radiation from all our cell-phones might reach, at most, Alpha Centauri!).
Then there is "dark energy". This is a misnomer. Einstein's Special Relativity tells us that energy and mass are equivalent. Hence, there is no way or need to consider matter and energy separately. In reality, dark energy is that "pressure" term in the stress tensor that I mentioned earlier. It can be equivalently considered to be the "cosmological constant". It is needed to explain some observed data. However, like dark matter, it is not evidence for the Big Bang. Note that I am using only mathematical descriptions for this piece of the stress tensor. This is because there is no physically observable analog of this quantity.
The Age of the Universe?
Now, if there is no evidence for the Big Bang, why is the theory so popular? I believe it is purely anthropocentric in nature. It comes from our need to find a beginning for everything -- just because each of us individual humans have had such a beginning -- a catastrophic beginning.
In this light, we can track the constantly changing estimate for the age of the universe. The Bible says it is anything from 3,000 to 6,000 years. Hindu texts talk about cycles within cycles in the time progression of the universe. One such cycle period (4,320,000,000 years) is close to what the Big Bang theory expects the age of the universe to be. Cosmologists have estimated the age to be anywhere from 10,000,000,000 years to 20,000,000,000 years. The most recent value comes from WMAP (Wilkinson Microwave Anisotropy Probe). It is 13,700,000,000 years.
The WMAP project is a remarkable experimental endeavor. Its weakness is in the single-mindedness of verifying the Big Bang theory alone. No attempt is made to fit the data to any other theory. Nonetheless, even if we were to go along with the data fitting to the Big Bang model alone, there is no evidence in the data for the advertized finite age of the universe. All that can be measured from the data is the time elapsed since the last scattering of the radiation to the present. This is the 13.7 billion years. The data has no way of telling what the time elapsed was from the instant of the Big Bang to the time of last scattering. This elapsed time is estimated as 380,000 years from theory. But there is no experimental verification of this. It could really be anything -- including infinity! Hence, the real age of the universe could be infinity -- it was never born.